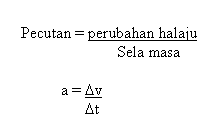
PECUTAN
Gerakan
jasad yang mengalami perubahan halaju atau mempunyai halaju yang tidak seragam
dikatakan mengalami pecutan. Halaju jasad dikatakan berubah sekiranya berlaku
salah satu daripada perubahan berikut;
ii.
Arah halaju
iii.
Magnitud dan arah halaju
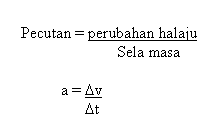
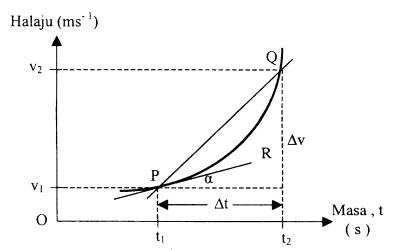
Pada
rajah 2.11, ditunjukkan bahawa magnitud halaju jasad v1 pada masa t1
berubah kepada v2 pada masa t2=(t
+ Dt),
maka pecutan purata jasad dalam sela masa Dt
adalah
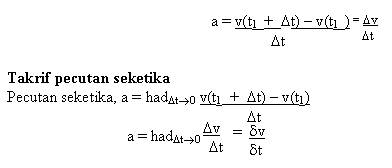
NOTA:
Sekiranya sela masa Dt
semakin kecil; dan menuju sifar garis PQ akan menghampiri garis tangen PR padas
titik t . Magnitud kecerunan garis
tangen ini ialah magnitud halaju seketika pada masa t
.
Gerakan dengan Pecutan Seragam
Pecutan
adalah kuantiti vektor. Pecutan seragam atau malar bererti magnitud dan arahnya
sentiasa malar. Daripada aspek takrifan pecutan pula, konsep berkenaan
menjelaskan perubahan halaju mesti malar, yang menunjukkan halaju v sentiasa
malar. Dengan ini gerakan dengan pecutan seragam adalah merupakan gerakan
menurut garis lurus. Penjelasan yang lalu menunjukkan bahawa satu jasad yang
bergerak dengan pecutan seragam adalagh mempunyai purata yang sama dengan
pecutan seketika.
A. Pecutan Sifar atau Halaju Seragam
Sekiranya jasad bergerak dengan magnitud dan
arah malar maka pecutan jasad adalah sifar. Oleh krana arah gerakan tidak
berubah, maka gerakan jasad adalah menurut garis lurus. Misalnya pada masa t
= 0. Kedudukan dan halaju
zarah x0 dan v0 dan pada masa t, halaju zarah ialah v,
maka,
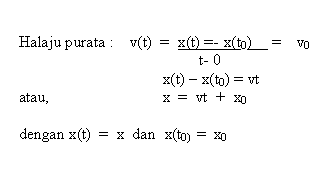
B. Pecutan Malar dan Tidak Sifar
Magnitud
halaju purata bagi pecutan malar boleh ditentukan daripada magnitud halaju
seketika pada masa ½ t jika t ialah tempoh masa pergerakan. Daripada rajah 12
dapat dinyatakan bahawa
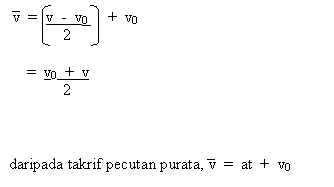
dengan menggantikan v kedalam persamaan (2.8), diperolehi
NOTA:
1.
pada persamaan di atas sebutan (x – x0) boleh digantikan
dengan sesaran, s.
2.
sering digunakan bahawa kedudukan awal jasad x0 = 0
ketika t = 0. Dalam hal ini jarak gerakan jasad dan sesaran adalah sama.