Lontaran – Gerakan pada satah

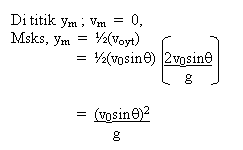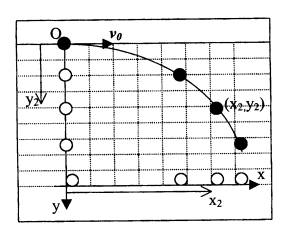
Pada rajah 2.18 ditunjukkan 1 objek dilancarkan secara mengufuk dari suatu aras di atas permukaan bumi. Lazimnya lintasan gerakan objek adalah tidak linear tetapi berbentuk lengkung, (parabola). Namum demikian gerakan ini dapat dianggap sebagai gabungan daripada 2 gerakan linear iaitu selari paksi-x dan paksi-y. Cuba bayangkan gerakan objek sekiranya diperhatikan dari atas dan dari sisi kiri.

Misalnya 2 titik A dan B terletak pada lintasan lontaran seperti ditunjukkan pada rajah di atas. Sekiranya vector kedudukan masing-masing titik dinyatakan sebagai;

r₁  =  x₁i  +  y₁j dan

r₂  =  x₂i  +  y₂j

maka sesaran jasad dari A ke B dapat dinyatakan dengan

dan pecutan seketika,

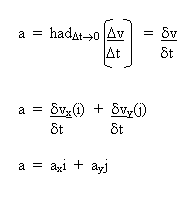
Daripada rajah 2.20 dapat diperhatikan walaupun arah v sentiasa berubah tapi arah v_x adalah sentiasa tetap. Dalam peristiwa lontaran, jasad hanya mengalami tarikan daya gravity yang arahnya ke bawah (paksi-y negatif). Dengamn ini pecutan jasad mempunyai

Komponen-y:    a_y  =  -gj

Komponen-x     a_x  =  0;  kerana a_x saling serenjang dengan a_y

Oleh itu gerakan jasad pada arah paksi-y adalah gerakan linear dengan pecutan seragam seperti gerakan jatuh bebas manakala gerakan pada arah paksi-x adalah gerakan linear dengan halaju malar.

  Andaikan suatu abjek dilontar dengan halaju awal v₀ dan arah q terhadap satah seperti ditunjukkan pada rajah 21. maka,

1.      komponen-x dan komponen-y bagi v₀ ialah

                        v_x  =  v₀kosq

                        v_y  =  v₀sinq

2. halaju jasad pada masa, t, v(t)

            komponen-x,   v_x  =  v_0x  +  a_xt

                                          =  v₀kosq

     dan komponen-y,     v_y  =  v₀ sinq - gt

     maka,  v(t)  =  (v_x²  +  v_y²)^1/2

3. Masa penerbangan

      Ialah masa bagi jasad mencapai julat lontaran. Atau masa bagi jasad melakukan

      gerakan dari titik lontaran hingga mencecah permukaan ufuk.

Nota:   Masa penerbangan boleh juga dikira berpandukan gerakan menegak. Iaitu jumlah masa bagi jasad mencapai ketinggian max dan turun semula mencecah permukaan ufuk (bumi).

Daripada persamaan, y  =  v₀  +  (1/2)a_yt²

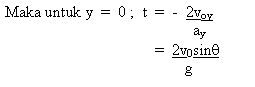
4. Julat jarak mengufuk

Ialah jarak mendatar yang dicapai objek semasa penerbangan.

Daripada persamaan,

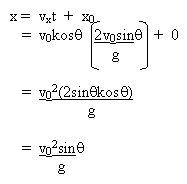
5. Tinggi maksimum, y_m.

     Ialah ketinggian maksimum pada arah y yang dicapai jasad dari titik lontaran.

[SEBELUM]  [SELEPAS] [MUKA UTAMA]